Security Testing
Tomaso Vasella

So funktioniert symmetrische Verschlüsselung
Es erscheint der Eindruck, dass oft allzu schnell auf die Aussagen Dritter gesetzt wird. Dies birgt gewisse Risiken, in dem Sinne, dass es sich schnell zu einfach gemacht wird und über die Zeit hinweg mehr Vertrauen als Wissen zur Thematik Verschlüsselung entstehen.
Gerade wenn neue Aussagen über die Stärke von Verschlüsselungen publiziert werden, kann unbegründeter Druck entstehen, auf die aktuell stärkste Verschlüsselungstechnologie zu wechseln zu müssen, obwohl dies evtl. zur gegebenen Zeit nicht zwingend notwendig ist. Sich an die Aussagen von Dritten zu halten und jeweils die stärkste Verschlüsselung zu wählen ist nicht falsch und entschieden besser, als sich mit der Thematik gar nicht auseinander zu setzen. Trotzdem sollten einige Konzepte der Verschlüsselung bekannt sein, um die sich stetig verändernde Situation der Thematik auf etwas bewussteren Entscheidungen anstatt Vertrauen zu stützen.
Für spezifische Fragen über die kryptographischen Stärken und Schwächen von Verschlüsselungs-Algorithmen respektive Implementationen, z.B. in Umgebungen mit begrenzten Ressourcen, sollten von vornhinein erfahrenen Kryptologen beigezogen werden. Und eine weitere goldene Regel vor weg: Eine eigene Implementation von kryptographischen Verfahren sollte man nur zu Übungszwecken anstreben. Kryptographische Verfahren in produktiven Systemen sollten nur durch erfahrene und ausgewiesene Kryptologen implementiert werden.
In diesem Artikel soll anhand einiger aktuellen Beispiele auf verschiedene Begriffe und Konzepte der symmetrischen Verschlüsselung eingegangen werden. Die erwähnten Konzepte sind nicht als Empfehlung zu verstehen, sondern sollen effektiv einige der Begriffe wie AE, MAC oder Mode of Operation vorstellen.
Die Mathematik und effektive Implementation von kryptographischen Verfahren werden nur angestreift oder ganz weggelassen. Die dazu vorgestellten Konzepte werden teils stark vereinfacht. Die verwendeten Illustrationen sollen helfen die Konzepte besser zu verstehen, am Ende des Artikels ist eine entsprechende Legende zu finden.
Die modernen symmetrischen Verschlüsselungsverfahren sind die im Prinzip die technische Weiterentwicklung der klassischen Mechanismen. Unter den klassischen Verfahren wird gerne die Cäsar-Verschlüsselung (ca. 50 v. Chr.) genannt, welche ein einfaches Substitutions-Verfahren darstellt.
Ein erstes Zeugnis von Verschlüsselung, wie von Forschern vermutet wird, ist die verschlüsselte Anleitung zu einer Tonglasur, geschrieben in Keilschrift auf einer Steintafel 2000 Jahre vor Christus aus Mesopotamien. Man geht davon aus, dass die Anleitung verschlüsselt wurde, um sich gegen Industriespionage zu schützen.
Die Symmetrie wird aus der Tatsache, dass für die Ver- und Entschlüsselung denselben geheimen Schlüssel K verwendet wird, abgeleitet, wie in der folgenden Abbildung dargestellt. (Eine Legende der genutzten Symbole findet sich im Anhang dieses Artikels.)
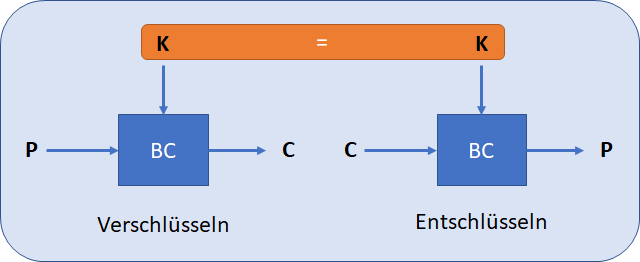
Die symmetrischen Verfahren bleiben aktuell die erste Wahl für die Verschlüsselung von grösseren Datenvolumen, schlicht weil diese meist performanter sind. Auch wird grundsätzlich zwischen Hardware und Software Implementation von Verschlüsselung unterschieden, jedoch auch da werden in den meisten Anwendungsfälle die Performanceunterschiede stetig kleiner.
Die Tatsache jedoch, dass derselbe Geheim-Schlüssel für Ver- und Entschlüsselung verwendet wird, macht ein reines symmetrisches Verfahren ungeeignet für eine verschlüsselte Kommunikation. Denn wie sollte der geheime Schlüssel initial zwischen Sender und Empfänger ausgetauscht werden (Schlüsselverteilungsproblem)? In früheren Zeiten ging dies noch mit Boten und versiegelten Briefen, jedoch skalierte dies schlecht.
Daher wurde asymmetrische Verfahren eingeführt, welche typischerweise Anwendung für den Austauschen des Geheimschlüssels von symmetrischen Verfahren finden, was in einem hybriden Verfahren resultiert.
Klartext-Block P, zu einer definierten Blockgrösse, wird mit dem Schlüssel K und Blockchiffre BC zu einem Geheimtext C verschlüsselt, wie in der folgenden Abbildung dargestellt. Z.B. bei AES ist die Blockgrösse 128 Bit.
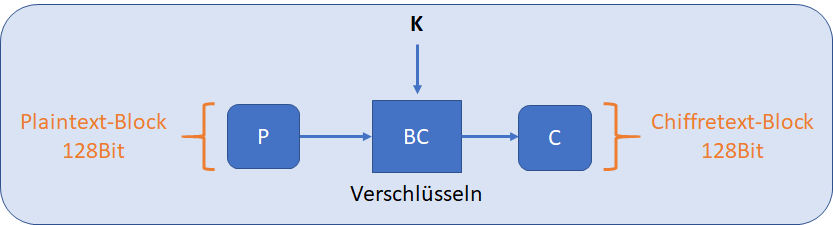
Die blockweise Verarbeitung verlangt eine weitere Komponente, um funktional zu sein, die High-Level Fragestellungen dazu sind:
Die obigen Fragen werden mit dem sogenannten Betriebsmodus (Mode of Operations) für Blockchiffren gelöst. Darum ist die Aussage, dass etwas mit AES verschlüsselt wurde ist, meist nicht komplett – es soll der Betriebsmodus mit angegeben werden. Warum? Da der Betriebsmodus nicht nur eine Funktion für die verarbeiten von Klartexten beliebiger Grösse ist, sondern auch Security-Features miteinbringt.
Ein eindrückliches Beispiel für Security-Features, welche “ausserhalb” des eigentlichen Verschlüsselungs-Algorithmus “hinzugefügt” werden sollte, ist unter der Phrase Everybody knows ECB mode is bad because we can see the penguin.
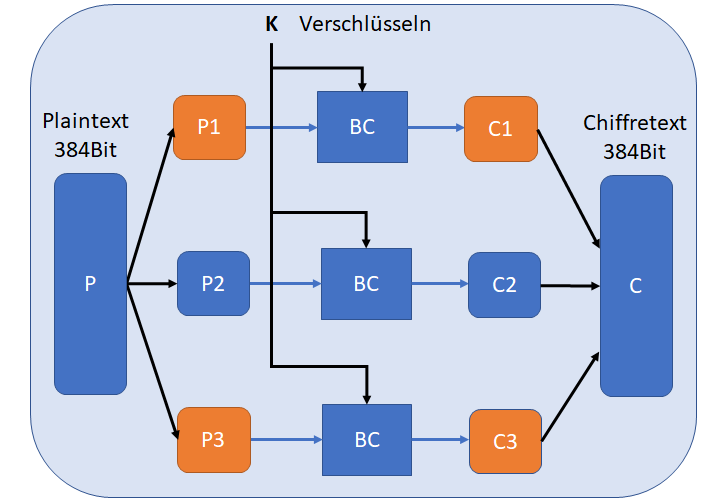
Der ECB-Betriebsmodus, der einfachste der Betriebs-Modi, sorgt dafür, dass ein Klartext beliebiger länge mit einer Blockchiffre verschlüsselt werden kann, dabei wird der Klartext in die nötige Blockgrösse formatiert und jeder Block nacheinander mittels BC-Algorithmus verschlüsselt, wie zuvor gezeigt.
Die nachfolgende Abbildung zeigt das Pinguin-Problem nachgebaut mit dem scip Logo: Das scip Logo verschlüsselt mit AES-ECB 128bit und als Vergleich noch einmal mit AES-CBC.

Die Konklusion aus dem Pinguin-Problem ist, dass identische Klartext-Blöcke identische Geheimtext-Blöcke produzieren. Also wenn P1 und P3 identisch sind, dann sind auch C1 und C3 identisch. Damit lassen sich gewisse Informationen aus dem Geheimtext gewinnen. Eine Art von Zufälligkeit ist von Nöten, um dem beizukommen.
Der Verschlüsselungsalgorithmus stellt eine sichere Transformation her. Bei AES mit Blockgrösse 128 Bit ohne Betriebsmodus also nur genau für einen 128 Bit Block.
Die Basis-Modi sollen einerseits sicherstellen, dass Klartext beliebiger länger verschlüsselt werden kann und einfach ausgedrückt, dass keine Muster im Geheimtext erkannt werde können. Auch wenn mehrmals derselbe Klartext mit demselben Schlüssel verschlüsselt wird, sollte jedes Mal eine “anderer” Geheimtext “entstehen”.
Um zu verhindern, dass Pattern entstehen, werden Methoden der Randomisierung angewandt. Damit wird eine Verschlüsselungalgorithmus wie AES in Kombination mit einem Betriebsmodus (ausser ECB) kryptographisch stärker. ECB (The Electronic Codebook) sollte, wie das obige Beispiel zeigt, nicht mehr verwendet werden.
CBC (Cipher Block Chaining Mode), siehe nachfolgende Abbildung, funktioniert ähnlich wie ECB, verknüpft (chaining) aber jeden Block mit dem vorhergehenden. Für den ersten Block wird ein sogenannter randomisierter Initialisierungs-Vektor (IV) hergenommen, um so eine Art von Randomisierung hinzuzufügen. Dies sorgt dafür, dass identische Klartext-Blöcke nicht in identischen Geheimtext-Blöcke verschlüsselt werden. Auch wenn die Verschlüsselung zweimal für denselben Klartext und Schlüssel aufgerufen wird, wird durch den randomisierten IV und das Chaining der Geheimtext jedes Mal anders ausfallen.
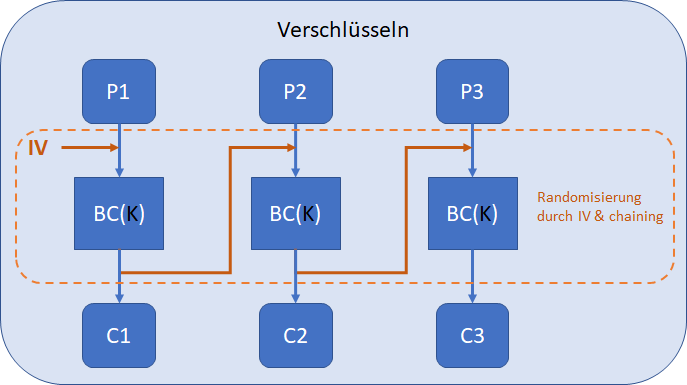
Für den CBC-Modus ist ein weiteres Verfahren namens Padding notwendig. Ist der Klartext kein Vielfaches der Blockgrösse, also ist z.B. der Klartext 132 Bit lang, kann ein erster 128 Bit Block erzeugt werden, für die übrigen 4 Bit Klartext wird aber ebenfalls ein 128 Bit Block benötigt, so müssen die 4 Bit mit 124 Bit auf 128 Bit aufgefüllt werden. Ein Effekt des Paddings ist, dass der Geheimtext immer etwas länger ist als der Klartext.
Eine weitere Methode, um die nötige Blockgrösse herzustellen, ist das CTS. Es ist etwas komplizierter, jedoch stellt es sicher, dass Geheimtext und Klartext gleich lang sind. Dies indem es, vereinfacht gesagt, die nötige Menge an Bits für das Padding vom zweitletzten Chiffreblock wegnimmt (stiehlt) und damit den letzten Klartext-Block auffüllt, bevor dieser mit der Menge benötigter Bits verschlüsselt wird.
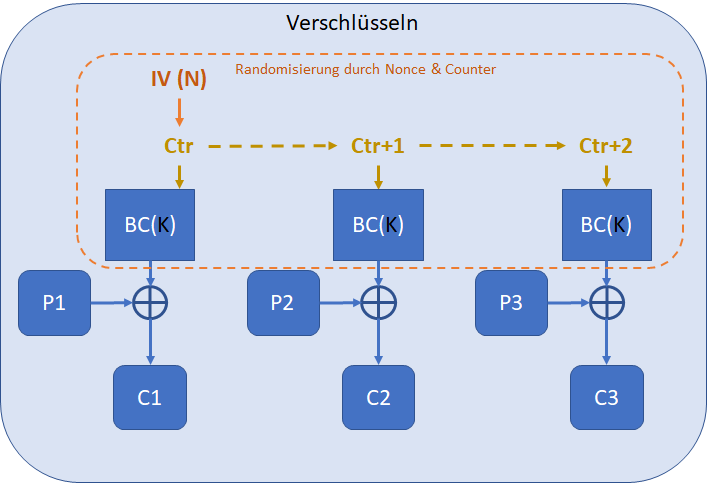
CTR (Counter Mode), siehe die nachfolgende Abbildung, macht aus einer Blockchiffre praktisch eine Stromchiffre. Ein Counter (jeder Block einer Message darf nicht denselben Counter-Wert haben) und Nonce (Number used only once, muss nicht zufällig aber einzigartig per Schlüssel K/Message sein) als IV werden mittels Blockchiffre zu einer Art Schlüsselstrom (KS) verschlüsselt. Der Schlüsselstrom wird anschliessend via XOR mit dem Klartext in den Geheimtext bitweise verschlüsselt (mehr dazu unter Stromchiffren). Damit entfällt das Bedürfnis von Paddingverfahren für Blockchiffren mit CTS-Modus.
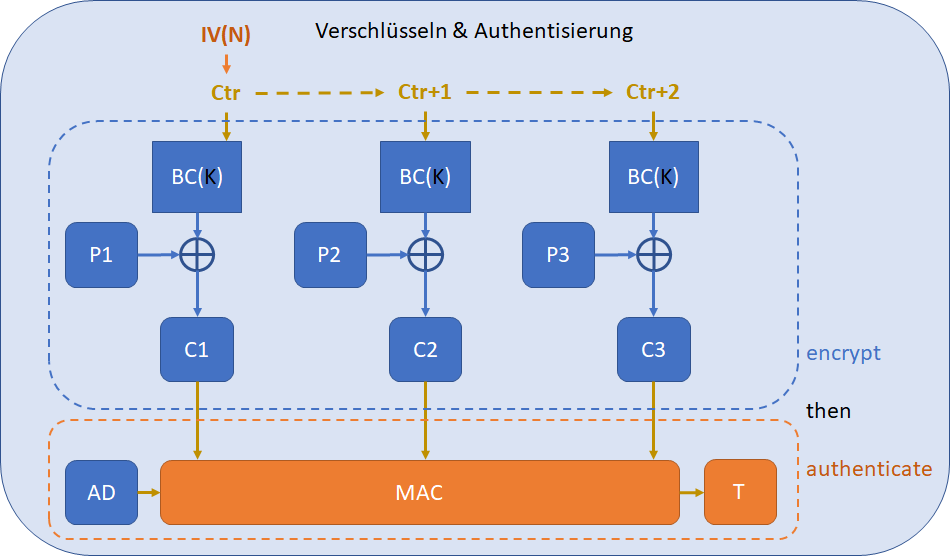
GCM (Galois/Counter Mode) basiert im Grunde auf CTR, integriert jedoch die Funktion Message Authentication (MAC). Dies soll sicherstellen, dass während der Entschlüsselung überprüft werden kann, ob die Daten im verschlüsselten Zustand, gewollt oder ungewollt, verändert wurden (Authentizität und Integrität der Daten), was in einer Authenticated Encryption (AE) resultiert.
Auch die Authentizität von nicht verschlüsselten Daten, wie Headerdaten (Associated Data) werden mit der MAC-Funktion von GCM authentisiert, was in Autenticated Encryption with Associated Data (AEAD) resultiert.
Die Verifizierung, ob sich Daten verändert haben, wird mit dem Wegman-Carter MAC Verfahren erreicht, das auf dem Hashingverfahren namens GHASH basiert. Das MAC-Verfahren erzeugt nach der Verschlüsselung (Encrypt-then-Authenticate) einen Authentication-Tag, welcher bei der Entschlüsselung ebenfalls berechnet werden kann. Stimmen diese überein, kann davon ausgegangen werden, dass die Daten nicht verändert wurden. GCM kann übrigens auch für die Authentisierung von nicht verschlüsselten Daten verwendet werden, dies wird dann GMAC (Galois Message Authentication Code) genannt.
CCM (Counter Modus with CBC-MAC) basiert wie der Name schon sagt auf dem CTR Modus und verwendet CBC als MAC Verfahren. Dabei wird im Gegensatz zu GCM erst authentisiert und dann verschlüsselt (Authenticate-then-Encrypt).
XTS (XEX-based Tweaked-Codebook Mode with Ciphertext Stealing) ist ein Modus, welcher für die Verschlüsselung von Daten auf einer Disk ausgelegt ist. Die Disk-Verschlüsselung stellt erweiterte Anforderungen an ein sicheres Verschlüsselungs-Konzept. Besonders die Unterteilung in Sektoren auf den Disks haben dazu einen grossen Einfluss, da jeder Sektor sicher, einzeln und performant ver- und entschlüsselt werden soll. Dazu kommt der Begriff Tweaked ins Spiel, respektive Tweakable Encryption (TE).
TE wird bei der Disk-Verschlüsselung benutzt, um den Sektor in das Verschlüsselungsverfahren mit ein zu beziehen. Damit kann eine ganze Disk mit demselben Schlüssel, aber eine Sektorspezifischen Wert als eine Art zusätzlichem Schlüssel (dem Tweak) verschlüsselt werden. Stromchiffren (wie auch Blockchiffre mit Counter Mode) sind aus gewissen Gründen für die Disk-Verschlüsselung ungeeignet.
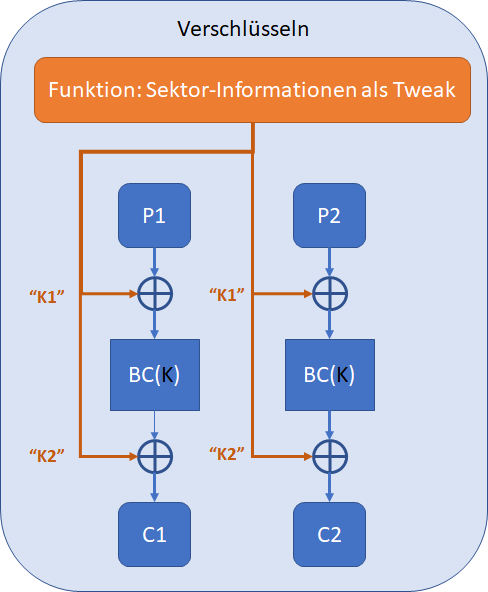
Der Basis Mode für XTS ist XEX (XOR-encrypt-XOR), was für die Verschlüsselung gleich drei Schlüssel verwendet, einer dieser Schlüssel kann daher der Tweak-Wert sein. Bei einer XEX-Implementation ohne Tweak wird dies mit Key Whitening erreicht, respektive werden vom dem Schlüssel K die Schlüssel K1 und K2 abgeleitet.
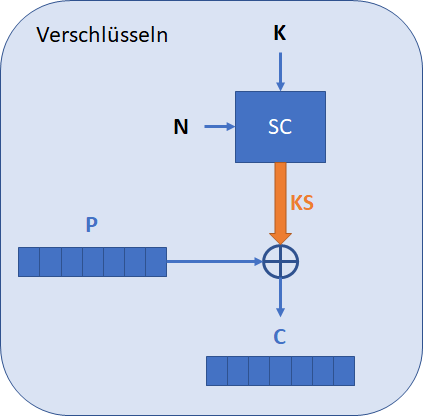
Eine Stromchiffre, wie der Name andeutet, verschlüsselt einen Strom von Daten, also Bit für Bit eines Klartexts. Dies, indem jedes Bit aus dem Klartext P mittels eins Bits aus dem sogenannten Schlüsselstrom KS zu dem Geheimtext C verschlüsselt wird. Der Schlüsselstrom wird aus einem geheimen Schlüssel K sowie aus einem Nonce N mittel der Stromchiffre SC generiert, siehe die nachfolgende Abbildung. Konkret wird dem Schlüssel und dem Nonce mittels einem Stromchiffre-Algorithmus ein pseudo-randomisierter Strom von Bits generiert.
Historisch wurden Stromchiffren als performanter bei Hardware-Implementationen gehandelt, da sie mit weniger Ressourcen (Anzahl Logik-Gatter) auskahmen. Heute hat sich dies zu einem gewissen Masse gegenüber den Blockchiffren relativiert, da diese heute ebenfalls schlanke Hardware Implementationen aufweisen und auch nicht zuletzt, weil die verfügbaren Ressourcen in den Hardwarechips stetig zunehmen.
Stromchiffren sollten denselben KS nicht zweimal einsetzen (respektive dasselbe Nonce mit demselben Schlüssel). Weiter sollte verhindert werden, dass der KS selbst sich nicht nach einer gewissen Periode wiederholt.
Die Länge des KS (eine Art Blockgrösse des KS) ist also fest definiert, z.B. ChaCha20 ist dies 512 Bytes. Dass hiesst, wenn ein Klartext grösser als 512 Bytes verschlüsselt werden soll, muss eine neue Instanz des Verschlüsselung-Algorithmus aufgerufen werden können. Dabei soll ein erneuter Aufruf randomisiert werden, da derselbe Schlüssel dafür verwendet wird.
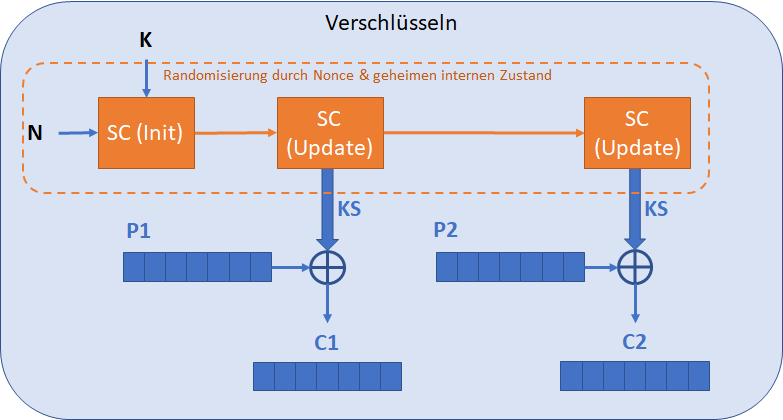
Stromchiffren können grob in zwei Typen unterschieden werden. Eine Stateful Stromchiffre (z.B. RC4) erzeugt einen geheimen internen Zustand mittels Schlüssel, Nonce und Algorithmus. Der Zustand dient als Ausgangslage für die Erzeugung des KS. Mittels einer Update-Funktion wird der Zustand über die Zeit verändert, um so die Erzeugung KS zu pseudo-randomisieren.
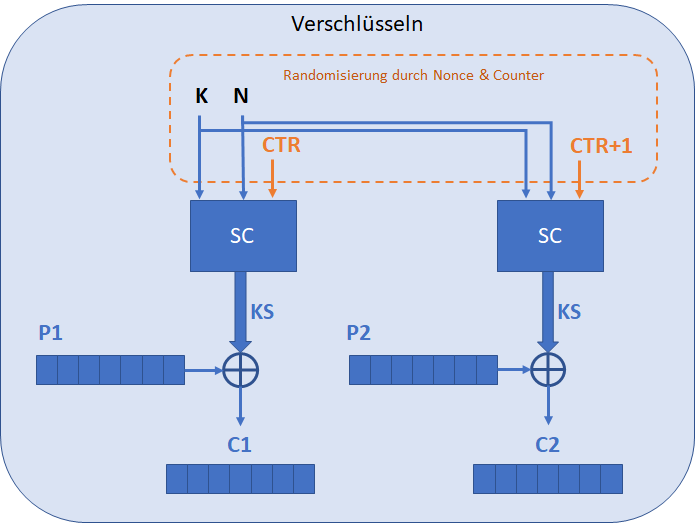
Eine counter-basierte Stromchiffre (z.B. Slasa20/ChaCha) löst die Randomisierung relativ simpel mit einem Counter für jede KS Periode, ähnlich wie der Counter-Mode für Blockchiffren.
Wie sieht es mit AE bei Stromchiffren aus? Aktuell empfohlene Stromchiffren kommen nicht mit einer integrierten AE-Funktion daher, wie bei den Blockchiffre Betriebsmodi. Aber natürlich kann zusätzlich ein generelles MAC-Verfahren implementiert werden, z.B. ChaCha20, Poly1305 (Encrypt-then-Mac).
Für das Basis-Verständnis zu symmetrischer Verschlüsselung kann folgendes zusammengefasst werden: Die symmetrischen Blockchiffre-Algorithmen bestehen aus einem Verschlüsselungsalgorithmus und einem geheimen Schlüssel, womit ein Klartext einer festen Blockgrösse in einen Geheimtext derselben Blockgrösse sicher transformieren kann. Durch den Einsatz eines Betriebsmodus können Klartexte beliebiger Grösse mittels mehrmaligen Aufrufens des Algorithmus verschlüsselt werden. Damit bei mehrmaligen Aufrufen keine Pattern entstehen, sollte der Betriebsmodus eine Art von Zufälligkeit (randomisierter IV, Noce IV, Chaining, …) erzeugen. Weiter können Betriebsmodi MAC-Verfahren (AE, AEAD) für die Verifikation der Integrität der Daten beinhalten und so weitere Security-Features einbauen.
Die symmetrischen Stromchiffren bestehen aus einem Verschlüsselung-Algorithmus, einem Nonce IV und geheimen Schlüssel, womit ein Schlüsselstrom erzeugt wird. Der Schlüsselstrom wird mittels XOR und Klartext zu einem Geheimtext verknüpft. Der Schlüsselstrom kann nur eine bestimme Länge haben. Daher wird auch bei Stromchiffren mehrmals der Vorgang aufgerufen, um Klartexte, welche länger als ein Schlüsselstrom sind, zu verschlüsseln. Der dafür notwendige Betriebsmodus ist bereits Teil der Stromchiffre. Aktuell empfohlene (BSI, ECRYPT) Stromchiffren bieten keine integrierte AE an, jedoch können Stromchiffren mit generellen MAC-Verfahren kombiniert werden.
Wer einen Schritt weiter gehen möchte, dem sei das Buch Serious Cryptography von Jean-Philippe Aumasson (ISBN 978-1-59327-826-7) empfohlen.
| Symbol | Beschreibung |
|---|---|
| K | geheimer Schlüssel |
| K1-K2 | Von K abgeleitet Schlüsselteile |
| P | Plaintext, Klartext |
| P1-P3 | Plaintext-Blöcke |
| C | Chiffretext, Geheimtext |
| C1-C3 | Chiffretext-Blöcke |
| BC | Blockchiffre |
| SC | Stromchiffre |
| IV | Initialisierungs Vektor |
| N | Nonce, Numnber only used once |
| Ctr | Counter |
| T | Tag, Authentication Tag |
| KS | Schlüsselstrom |
| ⊕ | XOR-Gatter |
Unsere Spezialisten kontaktieren Sie gern!

Tomaso Vasella

Eric Maurer

Marius Elmiger

Eric Maurer
Unsere Spezialisten kontaktieren Sie gern!