While SSLv3 is outdated, there is still a sizeable number of servers on the internet which show support for the protocol, either for backwards compatibility or through misconfiguration. This first article of a two-part series will introduce prerequisites for attacking SSLv3 and padding oracle basics. In the second article, a proof of concept to exploit SSLv3 connections is introduced.

SSLv3 is affected by a vulnerability called POODLE , which stands for “Padding Oracle On Downgraded Legacy Encryption”. Exploiting this requires an attacker to control the network traffic between the client and server. Such machine-in-the-middle (MITM) attack scenarios can be mostly put into action when the attacker is on the same network as the client or server. Examples could be an attacker luring a victim into a public Wi-Fi network set up for the attack or doing ARP spoofing on whatever shared network is available.

The attack requires both the client and server to support SSLv3. After the attacker has reached an MITM position, he may need to ensure that SSLv3 is used instead of any newer, more secure protocol. Clients such as browsers will try to use the newest available shared protocol with the server. An attacker cannot directly manipulate the content of the TLS/SSL handshake because of integrity checks. However, an attacker can terminate the handshake at the right moment to signal to the client that the server is incompatible with whatever version of TLS or handshake the client is attempting. This method omits any manipulations to the content of the handshake packets.

After the client sends its initial ClientHello message to the server in which it specifies the highest protocol version it supports, the attacker drops the packet and responds to the client with a FIN-ACK packet. This tells the client that the packet was received but the server wants to terminate the connection.

SSLv3 Vulnerability

POODLE is a padding oracle vulnerability. Padding oracle vulnerabilities use the validation of padding to derive information on the plaintext of an encrypted message. Padding is used in block ciphers to make the length of plaintext a multiple of the block size. This is necessary because block ciphers work on full blocks. If the last bit of remaining plaintext at the end of a message does not fill an entire block, the block is padded. A common way to pad is described in the PKCS#7 standard, which specifies that each byte of padding is to be filled with the number bytes of padding. For example, if the block size is 16 bytes and the last bit of plaintext is only 10 bytes long, 6 bytes of padding are added where each byte contains a 6. When a message is decrypted and the padding is wrong, it is an indicator that the message is corrupt.

#example of padded plaintext
FooMessage\x06\x06\x06\x06\x06\x06

CBC Mode of Operation

SSLv3 uses the CBC mode of operation. When using CBC, each block of plaintext is XORed with the previous block of ciphertext before encryption. The first block is XORed with the initialization vector.

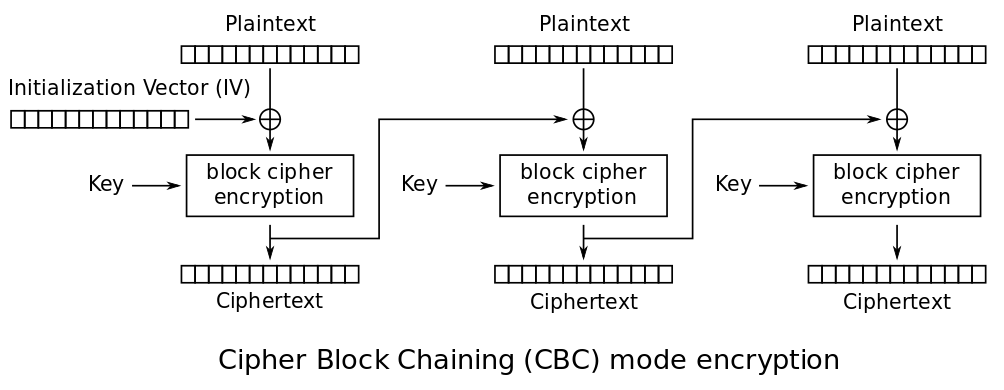
For reasons of simplicity this first example will use CBC with PKCS#7 padding. The formula for decrypting content is:

P_i = D(C_i) ⊕ C_i-1

Where P is plaintext, C is ciphertext, D() is the decryption operation and i is the block number. ⊕ is the XOR operator, programming languages often use ^. In a padding oracle attack the attacker sends a block of garbage ciphertext and appends a real block of ciphertext after it which he wishes to decrypt. The decryption operation performed on the server of the real block of cipher text is then:

P’_i = D(C_i) ⊕ C’_i-1

C' is the garbage ciphertext the attacker sends to the server. P' is the plaintext the server calculates after decrypting the real ciphertext and XORing it with the attacker’s garbage ciphertext.

C_i can be substituted with the corresponding encryption operation, E(P_i ⊕ C_i-1). This gives the equation:

P’_i = D(E(P_i ⊕ C_i-1)) ⊕ C’_i-1

Encryption and decryption are reversible operations which cancel each other out, so they can just be omitted here, resulting in:

P’_i = P_i ⊕ C_i-1 ⊕ C’_i-1

This equation contains the plaintext P_i which we are interested in with no decryption but only XOR operations. Since XOR is commutative, we can just shuffle the values around:

P_i = P’_i ⊕ C_i-1 ⊕ C’_i-1

Let us check if we have everything we need to solve the equation: C’_i-1 is the garbage ciphertext the attacker sends to the server and is known. C_i-1 is one of the real ciphertext blocks and is also known. P’_i is the plaintext value calculated by the server after decrypting a real ciphertext block and then XORing the result with our garbage ciphertext block. We do not know this value and this equation with two unknowns is not solvable. This is where the padding oracle comes into play.

Padding Oracle

The attacker sends his garbage ciphertext block together with the ciphertext block he wishes to decrypt appended after it. He can attempt to send this message with every possible value for the last byte of his garbage ciphertext block. If the decryption fails, the padding is incorrect. If the server manages to decrypt the message, it means the padding is valid. Thus, the padding is then \x01. It could also be \x02\x02 and with an even lower probability even \x03\x03\x03 and so on, but these scenarios are easily dealt with once we understand how the attack works. For now, we are going to assume the decrypted plaintext value the server receives after XORing the last byte of C_i with the last byte of our garbage ciphertext C_i-1 has to be \x01. Now we know one more value which we can insert into our equation, P’_i! We only know the last byte. This is designated with the [n] (i.e. P_i[n] is the n^th byte of P_i).

P_i[n] = P’_i[n] ⊕ C_i-1[n] ⊕ C’_i-1[n]

After we substitute P’_i[n]:

P_i[n] = 1 ⊕ C_i-1[n] ⊕ C’_i-1[n]

We successfully decrypted the last byte! To calculate the next byte, we follow the same principle. The attacker generates valid padding for the first and the second byte, i.e. \x02\x02. Before he can start brute forcing all 256 combinations to receive a \x02 of padding on the next byte, the last byte needs to be set to \x02. A brute force of both bytes requires probing a possibility space of 65536. This may still be doable, but the required effort increases exponentially with each byte. The third to last byte brings the count up to 16’777’216 combinations and the one after that to 4’294’967’296, which becomes unsustainable. Instead, we can repurpose out equation and solve for our “garbage” ciphertext C':

C’_i-1[n] = P’_i[n] ⊕ C_i-1[n] ⊕ P_i[n]

This is possible because we calculated and now know the plaintext value P_i[n]. We insert 2 for P’_i[n], because that’s what we want to solve for:

C’_i-1[n] = 2 ⊕ C_i-1[n] ⊕ P_i[n]

The attacker is now ready to find the next byte of plaintext. He sets the last byte of the garbage ciphertext block to the value we just calculated, which will result in a \x02 in the last byte of the next block of plaintext. Now, every combination of the second to last byte is sent to the server. If the server manages to successfully decrypt the content, we know that the second to last byte of the resulting plaintext in the next block is also “\x02” in order for the padding to be valid. We insert 2 for the value of P’_i[n] and retrieve the next plaintext byte.

P_i[n] = 2 ⊕ C_i-1[n] ⊕ C’_i-1[n]

An attacker can repeat this process until the entire block is decrypted. He doesn’t need to decrypt the blocks in order. The first block of ciphertext in a sequence is often decryptable. The first block of plaintext is XORed with an initialization vector (IV) before encryption since there is no preceding ciphertext block. In some implementations or misconfigurations however, an all-zero IV is used. In such a case, C_i-1 can just be omitted from the equation to calculate the plaintext of the first block.

Example

A simple example to illustrate a padding oracle vulnerability could be a website which encrypts session cookies with, for example, aes-128-cbc. The cookies contain claims, such as the user ID and the user’s role. If the website leaks cookie decryption failures in error messages, padding oracle attacks can be used to decrypt the cookie. Padding oracle attacks can also be used to encrypt arbitrary data, effectively allowing arbitrary claims to be properly encrypted, without knowing the private key. This would be more challenging if a random IV is used, since the first block or a block thereafter will be garbage.

Conclusion

Padding oracle attacks are an easy attack on cryptography to learn since they only include XOR operations. The next article will build on the basics established in this article and move to the specifics of the POODLE vulnerability in SSLv3.

About the Author

Ahmet Hrnjadovic is working in cybersecurity since 2017. There he is focused in topics like Linux, secure development and web application security testing. (ORCID 0000-0003-1320-8655)

Links

• https://datatracker.ietf.org/doc/html/rfc2315#section-10.3
• https://vuldb.com/?id.67791