Since we made you worry about our cryptographic future in our last article, we will now take this opportunity to show you a possible remedy against the evil attacks of quantum computers on our beloved asymmetric cryptography. Post-quantum cryptography is the scientific discipline of designing classical cryptographic algorithms that are resilient to both classical and quantum attacks. In this article, we will talk about one specific category of such post-quantum cryptography algorithms, lattice-based cryptography.

What is a lattice?

In simple terms, a lattice can be described as an infinite number of points on a periodically spaced grid. Before giving a more rigorous definition, we will first look at few mathematical concepts.

Vector

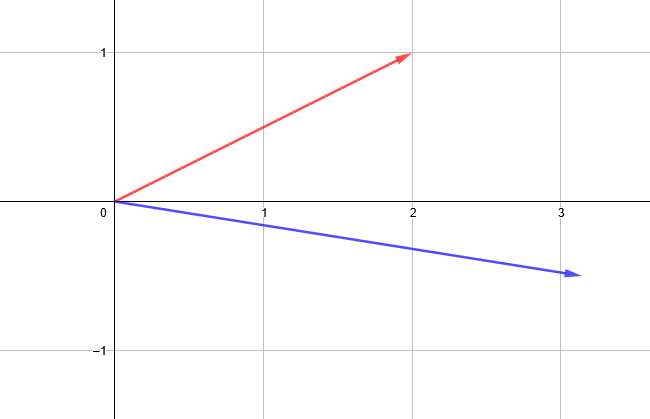
A vector is a mathematical object that has a length and a direction, much like an arrow drawn on a piece of paper. For the purpose of this article, we will limit ourselves to two-dimensional space and two-dimensional vectors. These 2D-vectors are described by two numbers. For example the red vector can be described as (2, 1) and the blue vector can be described as (3.14, -0.5).

Basis

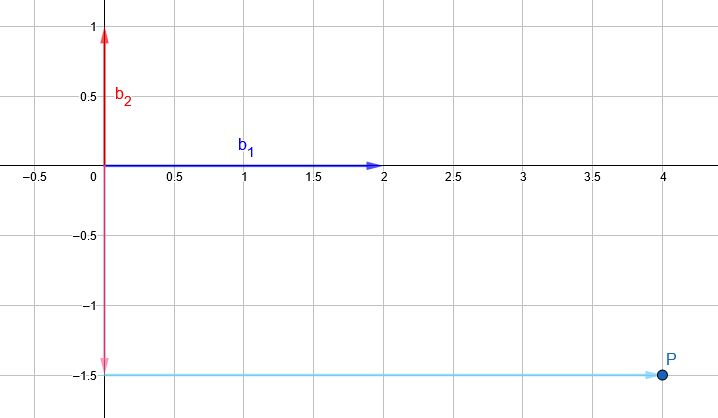
A basis is a set of vectors that allows us to reach any point in space by linearly combining them. For example, if we are given the basis:

B = {b₁ = (2, 0), b₂ = (0, 1)}

we can reach the point P = (4, -1.5) by linearly combining b₁ and b₂ in the following way:

P = 2 * (2, 0) – 1.5 * (0, 1) = (4, -1.5)

Note, that the number of bases for a given space is infinite. As long as two chosen vectors are linearly independent (one vector cannot be the result of a linear combination of the other), they can be used as a basis for the two-dimensional space.

Lattice

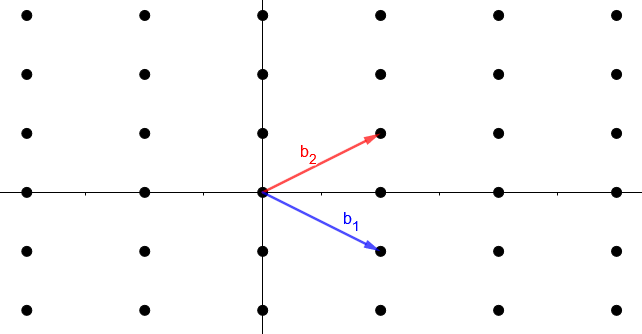
Now that we have a basic understanding of what a vector and a basis is, we can properly introduce a lattice. It is the set of all integer linear combinations of vectors from a basis { b₁,b₂ } of ℝ², which can be summarised as:

L = { a₁ b₁ + a₂ b₂ : a_i ∈ ℤ}

This means, that while the basis vectors b₁ and b₂ can have arbitrary real numbers as elements, like 1.5, 8 and π, the factors of the linear combination a₁ and a₂ can only be integers, like -3, 0 and 7. This definition of lattices gives them their periodic behaviour.

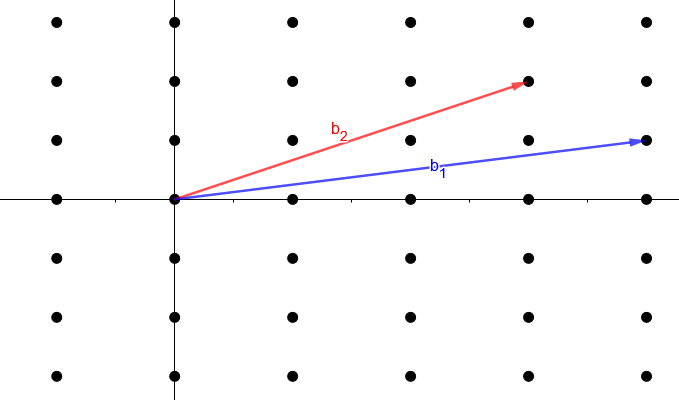
Much like with two-dimensional space, there is an infinite number of basis vectors that describe a given lattice. Below is an image of the same lattice as above but with different basis vectors.

Closest Vector Problem (CVP)

To use lattices as post-quantum-cryptographic tools, we must find problems that are hard to solve both on classical and on quantum computers. There are several such lattice problems, which are believed to be hard. We will look at the closest vector problem (CVP). In the CVP, the goal is to find the closest lattice point to a given point which is not necessarily on the lattice. To give further intuition on this problem, we will look at the concept of good and bad bases.

Bad Basis

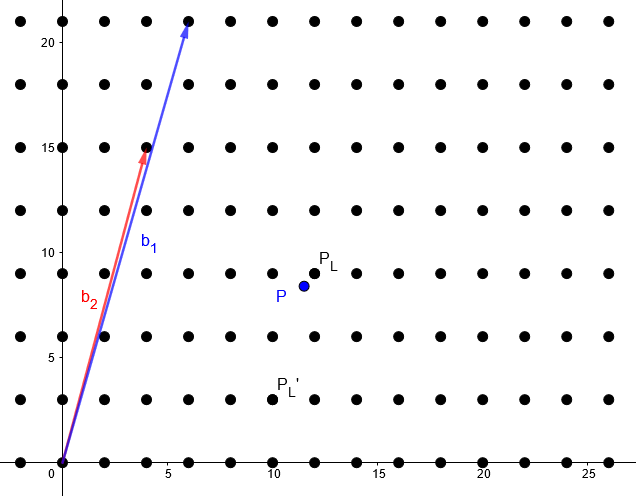
In this context, a bad basis is a lattice basis, for which it is hard to determine the closest point of a lattice for a given point. Consider the following basis:

B_bad = {b₁ = (6, 21), b₂ = (4, 15)}

Say we want to find the closest lattice point to the point P = (11.5, 8.4). Then we need to solve the following system of equations:

a₁ * (6, 21) + a₂ * (4, 15) ≈ (11.5, 8.4)

This can be solved by Gaussian elimination. The result of that calculation is a₁ = 23.15 and a₂ = -31.85. However, remember that we are looking for a lattice point and that lattice points only allow integer multiple of the basis coordinates. If we try to round to the nearest integer, we get a₁ ≈ 23 and a₂ ≈ -32. This gives us the approximative lattice point:

P_L’ = 23 * (6, 21) – 32 * (4, 15) = (10, 3)

This is not a great approximation for the actually closest lattice point P_L = (12, 9). This demonstration shows that our simple rounding algorithm is in general no good when using a bad basis.

Good Basis

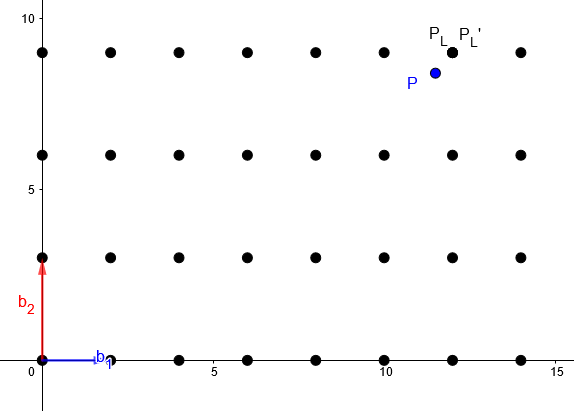
A good basis is a lattice basis which has short and nearly orthogonal vectors. We will see, that for such a basis, it is easy to determine the closest lattice point for a given point. Let us use the same lattice as before, but this time defined by the good basis:

B_good = {b₁ = (2, 0), b₂ = (0, 3)}

We still want to find the closest lattice point to the point P = (11.5, 8.4) and solve the linear system of equations:

a₁ * (2, 0) + a₂ * (0, 3) ≈ (11.5, 8.4)

The result is a₁ = 5.75 and a₂ = 2.8. If we again round to the nearest integer we get a₁ ≈ 6 and a₂ ≈ 3 and the following approximate lattice point:

P_L’ = 6 * (2, 0) + 3 * (0, 3) = (12, 9)

which is equal to the actual nearest point P_L = (12, 9). Thus for good basis, the rounding algorithm provides an accurate result.

Notice the asymmetry in hardness of the same problem between the two given bases. This asymmetry will allow us to construct an asymmetric cryptography protocol.

Goldreich-Goldwasser-Halevi (GGH) Lattice-Based Cryptosystem

We now present a simplified version of the GGH cryptosystem. It uses the CVP and the concept of good and bad bases to construct an asymmetric cryptography protocol.

Keys

The GGH cryptosystem has a public and a private key. The private key B = {b₁, b₂} is a good basis of the lattice L. The public key B’ = {b’₁, b’₂} is a bad basis of the lattice L.

Encryption

To encrypt a message m = (m₁, m₂), we generate a ciphertext by multiplying the message with the public key and adding a small, random error e = (e₁, e₂):

c = m * B’ + e = (m₁ * b’₁ + e₁, m₂ * b’₂ + e₂)

Note that the error is added, so that the ciphertext-point is not directly on the lattice. The error has to be small enough, so that the ciphertext-point is still closest to the original lattice point (without the error) in order to ensure correct decryption.

Decryption

In the decryption phase, we calculate the closest lattice point to the given ciphertext-point. For this, the private key and good lattice basis B is necessary. We use Gaussian elimination just like before to solve the linear system of equation:

a₁ * b₁ + a₂ * b₂ ≈ c

Then we round a₁ and a₂ to their nearest integer which gives us the original message m = (m₁, m₂).

Security of GGH

It was shown by Nguyen that the GGH encryption scheme has a design flaw where the ciphertext reveals information about the plaintext which then reduces the hardness of the CVP. Even though, the GGH scheme is not secure in practice, it is still an easy-to-understand example to show how the hardness of lattice problems can be turned into an encryption scheme.

Discussion

So, is that it? Are we saved from the unnerving future where quantum computers break all our cryptography and everyone can read everything? If the history of classical cryptography has taught us anything, it is that finding and implementing a secure encryption scheme is really hard. Add to that, that these post-quantum cryptography schemes must be resilient to both quantum and classical attacks and that they have had less time to mature and be tested and you see why it might be a long journey to true post-quantum cryptography. Nonetheless, the field has gained traction in the last couple of years and NIST is making progress on the standardization of the algorithms. Another promising option is quantum key distribution (QKD), which uses quantum physics to produce information-theoretically secure keys that cannot be broken by any physical device.

Disclaimer

This article is written for a broad audience and as such, some of the mathematical statements have been simplified and should not be used to derive further statements.

About the Author

Noah Berner obtained a bachelor’s degree in computer science and a master’s degree in quantum engineering from ETH Zurich. In addition to information security in complex data processing systems, his research interests include quantum key distribution protocols and physical quantum computing architectures. (ORCID 0000-0003-4320-097X)

Links

• https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.45.4818&rep=rep1&type=pdf
• https://en.wikipedia.org/wiki/Gaussian_elimination