SSLv3 ist zwar veraltet, wird jedoch trotzdem immer wieder angetroffen. Mögliche Gründe können Fehlkonfiguration oder der Bedarf nach Rückwärtskompatibilität sein. Dieser erste Artikel in einer zweiteiligen Serie wird Voraussetzungen zum Angreifen von SSLv3 und Padding-Oracle-Grundlagen behandeln. Der zweite Artikel stellt einen Proof-of-Concept zum Entschlüsseln von SSLv3-Verbindungen vor.

SSLv3 ist von einer Schwachstelle namens POODLE betroffen, was für Padding Oracle On Downgraded Legacy Encryption steht. Die Ausnutzung dieser Schwachstelle erfordert die Kontrolle des Netzwerkverkehrs zwischen Client und Server. Solch ein Machine-in-The-Middle-Angriff (MITM) kann meistens ausgeführt werden, wenn sich der Angreifer im selben Netzwerk wie der Client oder Server befindet. Beispiele dafür sind ein öffentliches WLAN-Netzwerk, welches für solch einen Angriff aufgesetzt wurde oder ARP-Spoofing, in Situationen wo das Netzwerk nicht kontrolliert wird.

Der Angriff erfordert die Unterstützung von SSLv3 beider Kommunikationspartner. Nachdem ein Angreifer zwischen diesen eine MITM-Position erlangt hat, wird er unter Umständen sicherstellen müssen, dass SSLv3 verwendet wird anstatt einer neueren Protokollversion. Clients, wie zum Beispiel Browser, werden versuchen die neueste mit dem Server geteilte Protokollversion zu verwenden. Ein Angreifer kann den TLS/SSL-Handshake aufgrund von Integritätsprüfungen nicht direkt manipulieren, um eine bestimmte Protokollversion zu erzwingen. Allerdings besteht die Möglichkeit den Handshake im richtigen Moment zu terminieren, um dem Client zu signalisieren, dass der Server nicht kompatibel ist mit der TLS-Version oder dem Handshake, welcher vom Client probiert wird. Mit diesem Vorgehen werden keine Inhalte von Paketen des Handshakes manipuliert.

Nachdem der Client seine initiale ClientHello Nachricht an den Server schickt, welche die höchste unterstützte Protokollversion spezifiziert, verwirft der Angreifer das Paket und antwortet dem Client mit einem FIN-ACK Paket. Dies gibt dem Client zu verstehen, dass der Server sein Paket empfangen hat, aber die Verbindung terminieren will.

SSLv3 Schwachstelle

POODLE ist eine Padding-Oracle-Schwachstelle. Padding-Oracle-Schwachstellen missbrauchen die Validierung des Paddings um Informationen über den Klartext einer verschlüsselten Nachricht abzuleiten. Padding wird in Block Ciphers verwendet um die Länge der zu verschlüsselnden Klartext-Nachricht ein Mehrfaches der Blockgrösse zu machen. Das ist nötig, weil Block Ciphers auf ganzen Blöcken operieren. Wenn am Schluss einer zu verschlüsselnden Klartext-Nachricht ein Teil übrigbleibt, der keinen ganzen Block füllt, wird Padding angehängt. Eine gängige Art Blöcken Padding anzuhängen ist im Standard PKCS#7 beschrieben, welcher definiert, dass jedes angehängte Byte des Paddings die Anzahl Bytes an Padding wiedergibt. Zum Beispiel wenn die Blockgrösse 16 Bytes ist und das letzte Stück Klartext ist nur 10 Bytes lang, werden 6 Bytes Padding angehängt, wobei jedes Byte den Wert 6 enthält. Wenn eine Nachricht entschlüsselt wird und das Padding ist falsch, ist das ein Indikator, dass die Nachricht korrupt ist.

#Beispielklartext mit Padding
FooMessage\x06\x06\x06\x06\x06\x06

CBC Operationsmodus

SSLv3 verwendet den CBC Operationsmodus. Bei CBC wird jeder Klartextblock vor der Verschlüsselung mit dem vorherigen Ciphertextblock “XORed”. Der erste Klartextblock, welcher keinen vorangehenden Ciphertextblock hat, wird dem Initialisierungsvektor (IV) “XORed”.

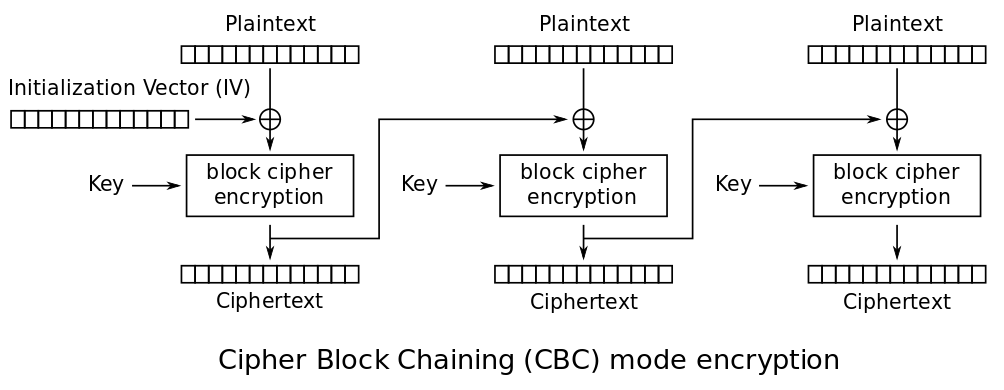
Der Einfachheit halber wird das erste Beispiel CBC mit PKCS#7 Padding verwenden. Die Formel für die Verschlüsselung lautet:

P_i = D(C_i) ⊕ C_i-1

P ist der Klartext (P für Plaintext), C ist Ciphertext, D() ist die Entschlüsselungsoperation und i ist die Blocknummer. ⊕ ist der XOR-Operator; Programmiersprachen verwenden dafür oft ^. Bei einem Padding-Oracle-Angriff nimmt ein Angreifer einen Block zufälligen Inhalt und fügt dahinter einen Block vom echten Ciphertext, welchen er entschlüsseln will, an. Diese Nachricht schickt er an den Server. Die Entschlüsselungsoperation, welche auf dem Server vom echten Ciphertextblock durchgeführt wird ist dann:

P’_i = D(C_i) ⊕ C’_i-1

C' ist der nichtssagende Inhalt, welcher an den Server gegangen ist. P' ist der Klartext welcher der Server erhält nachdem er den echten Ciphertext entschlüsselt und ihn dann “XORed” mit dem zufälligen Inhalt welcher der Angreifer vorangestellt hat.

C_i kann mit der korrespondierenden Verschlüsselungsoperation E(P_i ⊕ C_i-1) ersetzt werden. Das gibt die Gleichung:

P’_i = D(E(P_i ⊕ C_i-1)) ⊕ C’_i-1

Ver- und Entschlüsselung sind reversible Operationen, welche sich gegenseitig aufheben. Damit können sie hier weggelassen werden:

P’_i = P_i ⊕ C_i-1 ⊕ C’_i-1

Diese Gleichung enthält den Klartext des echten Ciphertexts, welchen wir haben wollen, ganz ohne Entschlüsselung und nur mit XOR-Operationen. Da XOR kommutativ ist, können die Werte beliebig herumgeschoben werden:

P_i = P’_i ⊕ C_i-1 ⊕ C’_i-1

Jetzt können wir prüfen, ob alle Werte zur Lösung der Gleichung vorhanden sind. C’_i-1 ist der zufällige Inhalt, welcher der Angreifer dem echten Ciphertextblock vorangestellt hat und ist bekannt. C_i-1 ist der echte Ciphertextblock welcher dem hier geschickten Ciphertextblock in der echten Nachricht vorangestellt war und ist ebenfalls bekannt. P’_i ist der Klartext, welcher der Server erhält, wenn er nach der Entschlüsselung des echten Ciphertextblocks die XOR Operation mit dem vorangestellten Inhalt des Angreifers durchführt. Wir kennen diesen Wert nicht und können diese Gleichung mit zwei Unbekannten nicht lösen. Hier kommt das Padding Oracle ins Spiel.

Padding Oracle

Der Angreifer schickt seinen zufälligen Inhalt zusammen mit dem Ciphertextblock welchen er entschlüsseln will. Er kann versuchen diese Nachricht mit jedem möglichen Wert im letzten Byte des vorangestellten Inhalts zu schicken. Wenn die Entschlüsselung fehlschlägt, ist das Padding in der resultierenden Nachricht falsch. Wenn der Server die Nachricht erfolgreich entschlüsseln kann, muss das Padding valide sein. In diesem Fall ist das Padding \x01. Es könnte auch \x02\x02 sein und mit einer noch niedrigeren Wahrscheinlichkeit auch \x03\x03\x03 und so weiter, aber diese Szenarios sind einfach zu handhaben, nachdem das Konzept klar ist. Für das jetzige Beispiel nehmen wir an, dass das Ergebnis der XOR-Operation des letzten Bytes unseres Inhalts und des letzten Byte des entschlüsselten Ciphertexts \x01 ergeben hat. Jetzt ist ein weiterer Wert bekannt, der in die Gleichung eingefügt werden kann, P’_i! Wir kennen nur das letzte Byte. Dies ist durch das [n] gekennzeichnet (d.h. P_i[n] ist das n^te Byte des Blocks P_i).

P_i[n] = P’_i[n] ⊕ C_i-1[n] ⊕ C’_i-1[n]

Nachdem wir P’_i[n] ersetzen:

P_i[n] = 1 ⊕ C_i-1[n] ⊕ C’_i-1[n]

Das erste Byte kann erfolgreich entschlüsselt werden. Um das nächste Byte zu entschlüsseln, kann das gleiche Vorgehen angewandt werden. Der Angreifer generiert jetzt allerdings valides Padding für die letzten 2 Bytes, also \x02\x02. Bevor der Angreifer alle 256 Kombinationen des vorletzten Bytes im eigenen Block an den Server schickt, um den Wert zu eruieren, welcher keinen Entschlüsselungsfehlerfehler ergibt, muss er zuerst das letzte Byte auf \x02 setzen. Ein Brute Force der beiden Bytes gleichzeitig muss einen Möglichkeitenraum von 65’536 durchsuchen. Das mag noch machbar sein, allerdings steigt der Aufwand exponentiell an mit 16’777’216 Kombinationen für das Letztdritte Byte, 4’294’967’296 für das nächste und ist damit nicht nachhaltig. Mit den vorliegenden Informationen kann der Wert des letzten Bytes, welcher beim Server nach Entschlüsselung und XOR eine \x02 ergibt, allerdings berechnet werden. Dafür kann die bereits verwendete Gleichung einfach umgestellt werden:

C’_i-1[n] = P’_i[n] ⊕ C_i-1[n] ⊕ P_i[n]

Das ist möglich, weil für dieses Byte der zugehörige Klartext, P_i[n], jetzt bekannt ist. Wir setzen für P’_i[n] 2 ein, weil das der Wert ist für den wir auflösen wollen.

C’_i-1[n] = 2 ⊕ C_i-1[n] ⊕ P_i[n]

Der Angreifer ist jetzt bereit das nächste Byte Klartext zu finden. Er setzt das letzte Byte des vorangestellten Inhalts auf den soeben berechneten Wert, welcher eine \x02 im letzten Byte des Plaintexts im nächsten Block ergibt. Jetzt wird die Nachricht mit jedem möglichen Wert im vorletzten Byte des vorangestellten Inhalts an den Server geschickt. Wenn der Server eine Nachricht erfolgreich entschlüsseln kann, wissen wir dass das vorletzte Byte im entschlüsselten Ciphertextblock auch eine \x02 ergeben hat damit das Padding stimmt. Wir fügen eine 2 als den Wert von P’_i[n] ein und erhalten den Klartextwert des nächsten Bytes.

P_i[n] = 2 ⊕ C_i-1[n] ⊕ C’_i-1[n]

Ein Angreifer kann diesen Prozess wiederholen, bis der ganze Block entschlüsselt ist. Die Ciphertextblöcke können in beliebiger Reihenfolge entschlüsselt werden. Der erste Ciphertextblock einer Sequenz ist oft nicht entschlüsselbar. Der erste Klartextblock wird mit dem Initialisierungsvektor (IV) XORed bevor er verschlüsselt wird, da es keinen vorangehenden Ciphertextblock gibt. In einigen Implementationen oder bei Misskonfigurationen wird ein IV aus nur Nullen verwendet. In so einem Fall kann C_i-1 bei der Berechnung des ersten Ciphertextblocks einfach aus der Gleichung entfernt werden.

Beispiel

Ein einfaches Beispiel um eine mögliche Padding-Oracle-Schwachstelle vorzustellen ist eine Webseite, welche ein verschlüsseltes Cookie verwendet, welches mit aes-128-cbc verschlüsselt wird. Das Cookie wird auf der Serverseite entschlüsselt, um die darin enthaltene Benutzer-ID und die Rolle des Benutzers zu eruieren. Wenn die Webseite Cookie-Entschlüsselungs-Fehlschläge über Fehlermeldungen preisgibt, kann ein Padding-Oracle-Angriff zur Entschlüsselung des Cookies verwendet werden. Padding-Oracle-Angriffe können auch zur Verschlüsselung von Daten verwendet werden, wodurch die Rechte des Benutzers im Cookie angepasst werden können. So kann ein gültiges Cookie valide verschlüsselt werden, ohne den privaten Schlüssel des Servers zu kennen. Die Schwierigkeit dieses Angriffs erhöht sich wenn ein zufälliger IV verwendet wird, da ein Block auf der Serverseite zwangsläufig zu nichtssagendem Inhalt entschlüsselt.

Fazit

Padding Oracles sind einfache Angriffe auf Kryptographie zu lernen weil sie nur XOR-Operationen beinhalten. Der nächste Artikel wird auf den hier eingeführten Grundlagen aufbauen und behandelt die Eigenheiten der POODLE-Schwachstelle in SSLv3.

Über den Autor

Ahmet Hrnjadovic arbeitet seit dem Jahr 2017 im Bereich Cybersecurity, wobei er sich auf die Bereiche Linux, sichere Programmierung und Web Application Security Testing fokussiert. (ORCID 0000-0003-1320-8655)

Links

• https://datatracker.ietf.org/doc/html/rfc2315#section-10.3
• https://vuldb.com/de/?id.67791