In einem unserer letzten Artikel haben wir Angst um unsere kryptographische Zukunft geschürt und wir möchten nun gerne eine mögliche Abhilfe zu den bösen Attacken der Quantencomputer auf unsere geliebte asymmetrische Kryptographie vorstellen. Post-Quanten-Kryptographie ist die wissenschaftliche Disziplin, die sich mit dem Design von klassischen kryptographischen Protokollen auseinandersetzt, die sowohl klassischen wie auch quantenbasierten Attacken standhält. In diesem Artikel werden wir uns auf eine spezifische Kategorie der Post-Quanten-Kryptographie konzentrieren, der gitterbasierten Kryptographie.

Was ist ein Gitter?

Einfach beschrieben kann man sagen, dass ein Gitter im mathematischen Sinne eine unendliche Anzahl Punkte auf einem periodisch angeordneten Raster ist. Bevor wir eine genauere Definition geben können, werden wir uns zuerst ein paar mathematische Konzepte anschauen.

Vektor

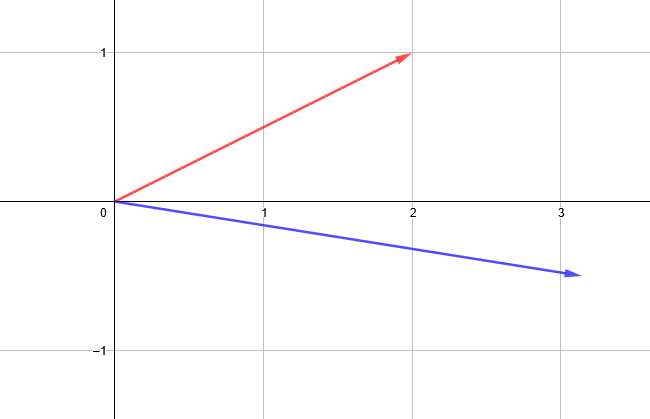
Ein Vektor ist ein mathematisches Konzept, das sowohl eine Länge wie auch eine Richtung hat. Man kann sich das wie ein auf Papier gezeichneter Pfeil vorstellen. In diesem Artikel werden wir uns auf den zweidimensionalen Raum und zweidimensionale Vektoren beschränken. Diese 2D-Vektoren können durch zwei Zahlen beschrieben werden. So ist zum Beispiel der rote Vektor definiert als (2, 1) während der blaue Vektor als (3.14, -0.5) definiert werden kann.

Basis

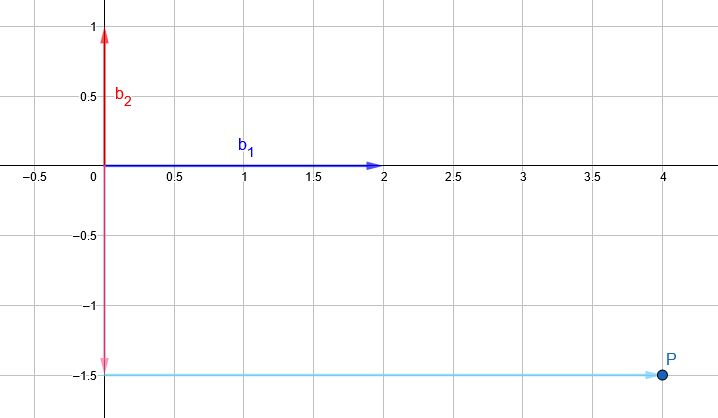
Eine Basis ist eine Liste von Vektoren, welche uns erlauben jeden beliebigen Punkt im Raum zu erreichen. Dazu setzen wir die Vektoren in eine Linearkombination. Wenn wir zum Beispiel die folgende Basis haben:

B = {b₁ = (2, 0), b₂ = (0, 1)}

dann können wir den Punkt P = (4, -1.5) erreichen, indem wir b₁ und b₂ wie folgt linear kombinieren:

P = 2 * (2, 0) – 1.5 * (0, 1) = (4, -1.5)

Es ist wichtig zu sehen, dass die Anzahl der Basen für einen gegebenen Raum unendlich ist. So lange die zwei gewählten Vektoren nicht voneinander linear abhängig sind (ein Vektor kann nicht als lineare Kombination des anderen erstellt werden), können sie als Basis für den zweidimensionalen Raum verwendet werden.

Gitter

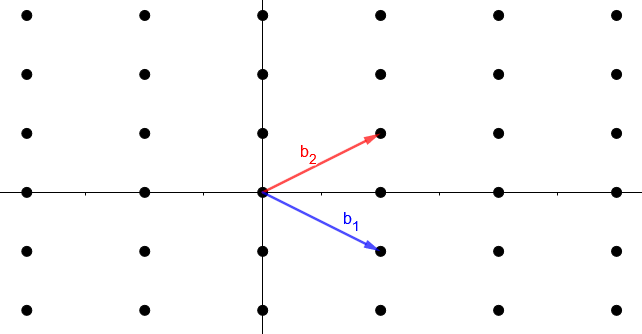
Nun da wir ein Grundverständnis über Vektoren und Basen erlangt haben, können wir das mathematische Konzept der Gitter einführen. Ein Gitter ist die Menge aller ganzzahligen Linearkombinationen der Vektoren einer Basis { b₁,b₂ } von ℝ², was zusammengefasst werden kann als:

L = { a₁ b₁ + a₂ b₂ : a_i ∈ ℤ}

Das bedeutet, dass die Basisvektoren b₁ und b₂ jede beliebige reelle Zahl als Element haben kann, wie zum Beispiel 1.5, 8 und π, die Faktoren der Linearkombination a₁ und a₂ müssen jedoch ganzzahlig sein, wie zum Beispiel -3, 0 und 7. Diese Definition gibt den Gittern ihre periodische Eigenschaft.

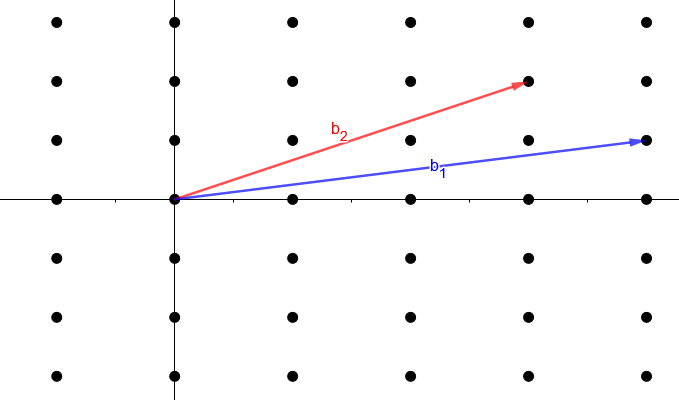
Ähnlich wie im zweidimensionalen Raum gibt es auch unendlich viele Basisvektoren, die ein vorgegebenes Gitter beschreiben. Im Bild unten sehen wir dasselbe Gitter wie oben, aber mit anderen Basisvektoren.

Closest Vector Problem (CVP)

Um Gitter als post-quanten-kryptographische Werkzeuge zu verwenden, müssen wir Probleme finden, die sowohl auf klassischen wie auch Quantencomputern schwer zu lösen sind. Es gibt einige solche Gitterprobleme, von denen man annimmt, das sie schwer sind. Wir werden uns mit dem Closest Vector Problem (CVP) auseinandersetzen. Im CVP ist das Ziel für einen gegebenen Punkt im Raum, der nicht zwingend auf dem Gitter liegt, den nächsten Punkt auf dem Gitter zu finden. Um dies besser zu illustrieren, führen wir nun die Konzepte der guten und schlechten Basen ein.

Schlechte Basis

In diesem Kontext bedeutet schlecht, dass es für eine schlechte Gitterbasis schwierig ist, für einen gegebenen Punkt den nächsten Gitterpunkt zu finden. Schauen wir uns die folgende Basis an:

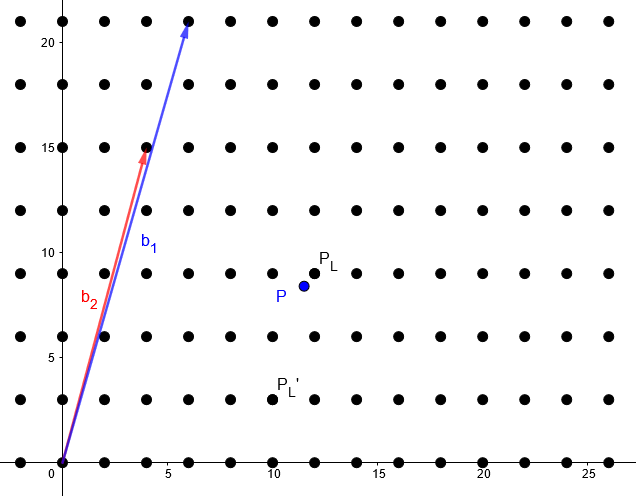
B_schlecht = {b₁ = (6, 21), b₂ = (4, 15)}

Wir wollen nun den nächsten Gitterpunkt zu dem gegebenen Punkt P = (11.5, 8.4) finden. Dazu können wir das folgende Gleichungssystem lösen:

a₁ * (6, 21) + a₂ * (4, 15) ≈ (11.5, 8.4)

Das Gleichungssystem kann durch das Gausssches Eliminationsverfahren gelöst werden. Das Resultat ist a₁ = 23.15 und a₂ = -31.85. Wir erinnern uns, dass wir einen Gitterpunkt suchen und Gitterpunkte nur ganzzahlige Vielfache der Basiskoordinaten sein dürfen. Wenn wir nun zu der nächsten Zahl runden, erhalten wir a₁ ≈ 23 und a₂ ≈ -32. Dies gibt uns den folgenden approximierten Gitterpunkt:

P_L’ = 23 * (6, 21) – 32 * (4, 15) = (10, 3)

Dies ist keine gute Approximation für den tatsächlich nächsten Gitterpunkt P_L = (12, 9). Dies zeigt, dass unser simpler Rundungsalgorithmus generell keine guten Ergebnisse liefert, wenn wir nur eine schlechte Basis zur Verfügung haben.

Gute Basis

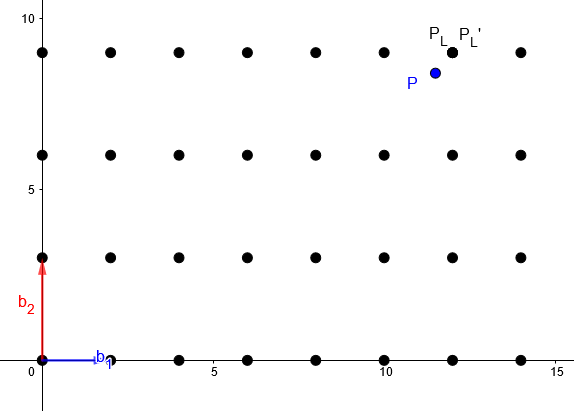
Eine gute Gitterbasis hat kurze und fast orthogonale Vektoren. Wir werden sehen, dass es mit einer solchen Basis einfach ist den nächsten Gitterpunkt für einen gegebenen Punkt im Raum zu bestimmen. Wir wiederholen den vorherigen Schritt, nur diesmal mit einer guten Basis:

B_gut = {b₁ = (2, 0), b₂ = (0, 3)}

Wir wollen immer noch den nächsten Gitterpunkt zu dem Punkt P = (11.5, 8.4) finden und lösen wieder das lineare Gleichungssystem:

a₁ * (2, 0) + a₂ * (0, 3) ≈ (11.5, 8.4)

Das Resultat ist a₁ = 5.75 und a₂ = 2.8. Wenn wir nun wieder zu der nächsten Zahl hin runden erhalten wir a₁ ≈ 6 und a₂ ≈ 3, sowie den folgenden approximierten Gitterpunkt:

P_L’ = 6 * (2, 0) + 3 * (0, 3) = (12, 9)

Dieser ist äquivalent zu dem tatsächlichen nächsten Gitterpunkt P_L = (12, 9). Für eine gute Basis gibt der Rundungsalgorithmus also ein genaues Resultat.

Die Asymmetrie in der Schwierigkeit des Problems zwischen den beiden Basen wird uns nun erlauben ein asymmetrisches Kryptographieprotokoll zu definieren.

Goldreich-Goldwasser-Halevi (GGH) Gitterbasiertes Kryptographiesystem

Wir führen nun eine vereinfachte Version des GGH Kryptosystems ein. Es verwendet das CVP und das Konzept der guten und schlechten Basen, um ein asymmetrisches Kryptographieprotokoll zu konstruieren.

Schlüssel

Das GGH Kryptosystem hat einen öffentlichen und einen geheimen Schlüssel. Der geheime Schlüssel B = {b₁, b₂} ist eine gute Basis für das Gitter L. Der öffentliche Schlüssel B’ = {b’₁, b’₂} ist eine schlecte Basis des Gitters L.

Verschlüsselung

Um eine Nachricht m = (m₁, m₂) zu verschlüsseln generieren wir den Geheimtext indem wir die Nachricht mit dem öffentlichen Schlüssel multiplizieren und einen kleinen, zufälligen Fehler e = (e₁, e₂) addieren:

c = m * B’ + e = (m₁ * b’₁ + e₁, m₂ * b’₂ + e₂)

Der Fehler wird hinzuaddiert, um zu verhindern, dass der Geheimtextpunkt auf dem Gitter landet. Der Fehler muss klein genug sein damit der Geheimtextpunkt immer noch am nächsten zum dem originalen Gitterpunkt (ohne den Fehler) liegt, um eine korrekte Entschlüsselung zu garantieren.

Entschlüsselung

Um den Geheimtext zu entschlüsseln, berechnen wir den nächsten Gitterpunkt zu dem gegebenen Geheimtextpunkt. Wir brauchen dafür den geheimen Schlüssel (die gute Gitterbasis) B. Danach wenden wir wie schon zuvor das Gausssche Eliminationsverfahren an, um das lineare Gleichungssystem zu lösen:

a₁ * b₁ + a₂ * b₂ ≈ c

Wenn wir nun a₁ und a₂ zu der nächsten Zahl hin runden erhalten wir die ursprüngliche Nachricht m = (m₁, m₂).

Sicherheit von GGH

Nguyen hat gezeigt, dass das GGH Verschlüsselungsverfahren Schwächen hat, weil dessen Geheimtext Informationen über die verschlüsselte Nachricht preisgibt und dadurch ein einfacher zu lösendes CVP kreiert. Auch wenn das GGH-Protokoll in der Praxis unsicher ist, bietet es doch ein gutes Beispiel, um das Umwandeln von harten Gitterproblemen in Kryptographieverfahren zu demonstrieren.

Diskussion

Also wars das? Sind wir nun gerettet von der düsteren Zukunft in der Quantencomputer all unsere Kryptographie knacken und jeder alles lesen kann? Wenn uns die Geschichte eines lehrt, so ist es, dass das Finden und Implementieren von sicherer Verschlüsselung sehr schwierig ist. Hinzu kommt noch, dass die Post-Quanten-Kryptographie-Verfahren sowohl gegen Quanten- wie auch klassischen Angriffen resilient sein muss und dass sie weniger Zeit hatten, um sich zu beweisen und getestet zu werden. Da sieht man, dass es noch eine lange Reise sein kann bevor wir wahre Post-Quanten-Kryptographie haben. Es soll aber auch gesagt sein, dass die Disziplin in den letzten Jahren einiges an Schwung gewonnen hat und NIST in der Standardisierung der Verfahren Fortschritte macht. Eine andere vielversprechende Option ist der Quantenschlüsselaustausch (QKD), welcher Quantenphysik nutzt, um informationstheoretisch sichere Schlüssel zu generieren welche von keinem physischen Gerät geknackt werden können.

Haftungsausschluss

Da sich dieser Artikel an ein breites Publikum wendet, wurden einige mathematische Aussagen vereinfacht und sollten nicht in der hier präsentierten Form verwendet werden, um weitere Aussagen herzuleiten.

Über den Autor

Noah Berner schloss sein Studium an der ETH Zürich mit einem Bachelor of Science in Informatik und einem Master of Science in Quantum Engineering ab. Neben der Informationssicherheit in komplexen Datenverarbeitungssystemen gehören Quantum-Key-Distribution-Protokolle und physische Quantencomputer-Architekturen zu seinen Forschungsinteressen. (ORCID 0000-0003-4320-097X)

Links

• https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.45.4818&rep=rep1&type=pdf
• https://de.wikipedia.org/wiki/Gau%C3%9Fsches_Eliminationsverfahren